Show Joint Probability of Markov Chain Is Exponential Family

Probability concept

This article is nigh the mathematical properties of continuous-time Markov bondage. For the general field of written report, see Markov chain.

A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will alter state according to an exponential random variable and then motility to a different land as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the to the lowest degree value of a set of exponential random variables, one for each possible state it tin can movement to, with the parameters determined by the electric current state.

An example of a CTMC with three states ${\displaystyle \{0,one,two\}}$ is as follows: the process makes a transition later the corporeality of time specified by the holding time—an exponential random variable ${\displaystyle E_{i}}$ , where i is its electric current land. Each random variable is independent and such that ${\displaystyle E_{0}\sim {\text{Exp}}(vi)}$ , ${\displaystyle E_{1}\sim {\text{Exp}}(12)}$ and ${\displaystyle E_{two}\sim {\text{Exp}}(18)}$ . When a transition is to be made, the process moves according to the jump chain, a discrete-time Markov chain with stochastic matrix:

${\displaystyle {\brainstorm{bmatrix}0&{\frac {one}{ii}}&{\frac {1}{ii}}\\{\frac {1}{3}}&0&{\frac {2}{3}}\\{\frac {5}{6}}&{\frac {i}{6}}&0\end{bmatrix}}.}$

Equivalently, past the theory of competing exponentials, this CTMC changes state from state i according to the minimum of ii random variables, which are independent and such that ${\displaystyle E_{i,j}\sim {\text{Exp}}(q_{i,j})}$ for ${\displaystyle i\neq j}$ where the parameters are given past the Q-matrix ${\displaystyle Q=(q_{i,j})}$

${\displaystyle {\begin{bmatrix}-6&3&3\\4&-12&8\\15&3&-eighteen\end{bmatrix}}.}$

Each non-diagonal value can be computed equally the production of the original state's property time with the probability from the jump concatenation of moving to the given state. The diagonal values are chosen so that each row sums to 0.

A CTMC satisfies the Markov holding, that its behavior depends only on its current country and non on its past beliefs, due to the memorylessness of the exponential distribution and of discrete-time Markov chains.

Definition [edit]

A continuous-fourth dimension Markov chain (X _t ) _t ≥ 0 is defined by:^[1]

For i ≠j, the elements q _ij are non-negative and describe the rate of the procedure transitions from state i to state j. The elements q _ii could exist chosen to be zero, just for mathematical convenience a mutual convention is to cull them such that each row of ${\displaystyle Q}$ sums to cipher, that is:

${\displaystyle q_{2}=-\sum _{k\neq i}q_{ik}.}$

Note how this differs from the definition of transition matrix for discrete Markov bondage, where the row sums are all equal to one.

There are three other definitions of the procedure, equivalent to the one above.^[2]

Transition probability definition [edit]

Some other common manner to ascertain continuous-fourth dimension Markov bondage is to, instead of the transition rate matrix ${\displaystyle Q}$ , utilize the following:^[one]

Naturally, ${\displaystyle m_{ii}}$ must exist naught for all ${\displaystyle i}$ .

The values ${\displaystyle v_{i}}$ and ${\displaystyle m_{ij}}$ are closely related to the transition rate matrix ${\displaystyle Q}$ , past the formulas:

${\displaystyle v_{i}=\sum _{k\neq i}q_{ik}=-q_{two},{\text{ for all }}i,}$

${\displaystyle m_{ij}={\frac {q_{ij}}{\sum _{yard\neq i}q_{ik}}},{\text{ for all }}i\neq j.}$

Consider an ordered sequence of time instants ${\displaystyle t_{0}<t_{ane}<\dots <t_{n}}$ and usa recorded at these times ${\displaystyle i_{0},i_{1},\dots ,i_{n}}$ , then it holds that:

${\displaystyle \Pr(X_{t_{n+1}}=i_{n+1}\mid X_{t_{0}}=i_{0},X_{t_{1}}=i_{i},\ldots ,X_{t_{n}}=i_{n})=\Pr(X_{t_{due north+1}}=i_{n+1}\mid X_{t_{due north}}=i_{n})=p_{i_{north}i_{n+1}}(t_{north+1}-t_{due north})}$ ^{[ dubious – discuss ]}

where the p _ij is the solution of the forward equation (a starting time-club differential equation):

${\displaystyle P'(t)=P(t)Q}$

with initial condition P(0) being the identity matrix.

Infinitesimal definition [edit]

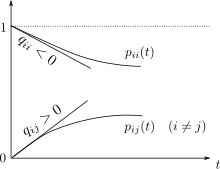
The continuous time Markov chain is characterized by the transition rates, the derivatives with respect to time of the transition probabilities between states i and j.

Permit ${\displaystyle X_{t}}$ be the random variable describing the state of the process at time t, and presume the process is in a land i at time t. Past definition of the continuous-time Markoff chain, ${\displaystyle X_{t+h}=j}$ is contained of values prior to instant ${\displaystyle t}$ ; that is, it is independent of ${\displaystyle \left(X_{s}:s<t\right)}$ . With that in mind, for all ${\displaystyle i,j}$ , for all ${\displaystyle t}$ and for small values of ${\displaystyle h}$ , the following holds:

${\displaystyle \Pr(Ten(t+h)=j\mid X(t)=i)=\delta _{ij}+q_{ij}h+o(h)}$ ,

where ${\displaystyle \delta _{ij}}$ is the Kronecker delta and the lilliputian-o notation has been employed.

The to a higher place equation shows that ${\displaystyle q_{ij}}$ can be seen equally measuring how quickly the transition from ${\displaystyle i}$ to ${\displaystyle j}$ happens for ${\displaystyle i\neq j}$ , and how quickly the transition abroad from ${\displaystyle i}$ happens for ${\displaystyle i=j}$ .

Leap chain/holding time definition [edit]

Define a discrete-time Markov chain Y _northward to depict the due northth jump of the process and variables S ₁, S _two, S ₃, ... to describe holding times in each of the states where S _i follows the exponential distribution with rate parameter −q _{Y i Y i} .

Properties [edit]

Communicating classes [edit]

Communicating classes, transience, recurrence and positive and nothing recurrence are divers identically as for detached-time Markov bondage.

Transient behaviour [edit]

Write P(t) for the matrix with entries p _ij = P(Ten _t  =j |X ₀ =i). Then the matrix P(t) satisfies the forward equation, a first-order differential equation

${\displaystyle P'(t)=P(t)Q}$

where the prime denotes differentiation with respect to t. The solution to this equation is given by a matrix exponential

${\displaystyle P(t)=e^{tQ}}$

In a simple instance such every bit a CTMC on the state space {i,2}. The general Q matrix for such a process is the following 2 × ii matrix with α,β > 0

${\displaystyle Q={\begin{pmatrix}-\alpha &\alpha \\\beta &-\beta \terminate{pmatrix}}.}$

The to a higher place relation for forward matrix can be solved explicitly in this case to give

${\displaystyle P(t)={\brainstorm{pmatrix}{\frac {\beta }{\blastoff +\beta }}+{\frac {\blastoff }{\blastoff +\beta }}e^{-(\alpha +\beta )t}&{\frac {\alpha }{\alpha +\beta }}-{\frac {\blastoff }{\alpha +\beta }}e^{-(\alpha +\beta )t}\\{\frac {\beta }{\alpha +\beta }}-{\frac {\beta }{\alpha +\beta }}east^{-(\blastoff +\beta )t}&{\frac {\alpha }{\blastoff +\beta }}+{\frac {\beta }{\alpha +\beta }}e^{-(\alpha +\beta )t}\end{pmatrix}}}$

Yet, straight solutions are complicated to compute for larger matrices. The fact that Q is the generator for a semigroup of matrices

${\displaystyle P(t+due south)=eastward^{(t+s)Q}=east^{tQ}e^{sQ}=P(t)P(s)}$

is used.

Stationary distribution [edit]

The stationary distribution for an irreducible recurrent CTMC is the probability distribution to which the procedure converges for large values of t. Find that for the two-state process considered earlier with P(t) given by

${\displaystyle P(t)={\brainstorm{pmatrix}{\frac {\beta }{\blastoff +\beta }}+{\frac {\blastoff }{\alpha +\beta }}e^{-(\alpha +\beta )t}&{\frac {\alpha }{\alpha +\beta }}-{\frac {\alpha }{\blastoff +\beta }}eastward^{-(\alpha +\beta )t}\\{\frac {\beta }{\blastoff +\beta }}-{\frac {\beta }{\blastoff +\beta }}eastward^{-(\alpha +\beta )t}&{\frac {\alpha }{\alpha +\beta }}+{\frac {\beta }{\blastoff +\beta }}east^{-(\blastoff +\beta )t}\end{pmatrix}}}$

every bit t → ∞ the distribution tends to

${\displaystyle P_{\pi }={\brainstorm{pmatrix}{\frac {\beta }{\alpha +\beta }}&{\frac {\blastoff }{\alpha +\beta }}\\{\frac {\beta }{\blastoff +\beta }}&{\frac {\blastoff }{\alpha +\beta }}\terminate{pmatrix}}}$

Find that each row has the same distribution as this does not depend on starting land. The row vector π may be institute past solving^[three]

${\displaystyle \pi Q=0.}$

with the additional constraint that

${\displaystyle \sum _{i\in Southward}\pi _{i}=one.}$

Example ane [edit]

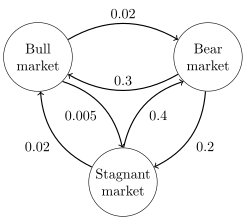
Directed graph representation of a continuous-time Markov chain describing the state of financial markets (notation: numbers are made-up).

The image to the correct describes a continuous-time Markov chain with state-space {Bull marketplace, Behave market place, Stagnant market} and transition rate matrix

${\displaystyle Q={\begin{pmatrix}-0.025&0.02&0.005\\0.three&-0.5&0.2\\0.02&0.4&-0.42\finish{pmatrix}}.}$

The stationary distribution of this chain can be found by solving ${\displaystyle \pi Q=0}$ , subject to the constraint that elements must sum to one to obtain

${\displaystyle \pi ={\begin{pmatrix}0.885&0.071&0.044\stop{pmatrix}}.}$

Case 2 [edit]

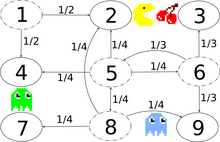
Transition graph with transition probabilities, exemplary for the states ane, 5, 6 and 8. At that place is a bidirectional secret passage between states 2 and 8.

The image to the correct describes a discrete-time Markov chain modeling Pac-Man with state-infinite {ane,2,3,4,5,6,seven,8,9}. The histrion controls Pac-Man through a maze, eating pac-dots. Meanwhile, he is being hunted by ghosts. For convenience, the maze shall be a small 3x3-filigree and the monsters movement randomly in horizontal and vertical directions. A clandestine passageway between states 2 and 8 can be used in both directions. Entries with probability zero are removed in the following transition charge per unit matrix:

${\displaystyle Q={\begin{pmatrix}-i&{\frac {ane}{2}}&&{\frac {one}{two}}\\{\frac {1}{4}}&-1&{\frac {1}{4}}&&{\frac {1}{4}}&&&{\frac {1}{4}}\\&{\frac {ane}{2}}&-1&&&{\frac {i}{2}}\\{\frac {one}{iii}}&&&-1&{\frac {1}{3}}&&{\frac {1}{3}}\\&{\frac {ane}{4}}&&{\frac {1}{four}}&-ane&{\frac {1}{iv}}&&{\frac {1}{4}}\\&&{\frac {1}{iii}}&&{\frac {i}{iii}}&-1&&&{\frac {i}{3}}\\&&&{\frac {1}{2}}&&&-1&{\frac {1}{2}}\\&{\frac {ane}{4}}&&&{\frac {1}{4}}&&{\frac {1}{4}}&-1&{\frac {1}{4}}\\&&&&&{\frac {1}{ii}}&&{\frac {1}{2}}&-1\stop{pmatrix}}}$

This Markov concatenation is irreducible, because the ghosts can fly from every country to every country in a finite amount of time. Due to the undercover passageway, the Markov chain is also aperiodic, because the monsters can move from any country to any state both in an fifty-fifty and in an uneven number of country transitions. Therefore, a unique stationary distribution exists and can be found by solving ${\displaystyle \pi Q=0}$ , subject to the constraint that elements must sum to 1. The solution of this linear equation subject to the constraint is ${\displaystyle \pi =(vii.7,xv.4,seven.7,xi.5,15.four,11.5,7.vii,xv.4,vii.7)\%.}$ The central state and the border states two and viii of the next underground passageway are visited almost and the corner states are visited least.

Fourth dimension reversal [edit]

For a CTMC 10 _t , the time-reversed procedure is defined to be ${\displaystyle {\hat {Ten}}_{t}=X_{T-t}}$ . By Kelly's lemma this procedure has the same stationary distribution every bit the forrad process.

A chain is said to be reversible if the reversed process is the aforementioned as the forrard procedure. Kolmogorov's criterion states that the necessary and sufficient condition for a procedure to exist reversible is that the product of transition rates around a closed loop must be the aforementioned in both directions.

Embedded Markov chain [edit]

One method of finding the stationary probability distribution, π, of an ergodic continuous-time Markov concatenation, Q, is past showtime finding its embedded Markov concatenation (EMC). Strictly speaking, the EMC is a regular detached-time Markov chain, sometimes referred to as a jump process. Each element of the one-footstep transition probability matrix of the EMC, Due south, is denoted by southward _ij , and represents the conditional probability of transitioning from state i into state j. These conditional probabilities may be found past

${\displaystyle s_{ij}={\begin{cases}{\frac {q_{ij}}{\sum _{thousand\neq i}q_{ik}}}&{\text{if }}i\neq j\\0&{\text{otherwise}}.\end{cases}}}$

From this, Due south may exist written as

${\displaystyle S=I-\left(\operatorname {diag} (Q)\right)^{-1}Q}$

where I is the identity matrix and diag(Q) is the diagonal matrix formed by selecting the main diagonal from the matrix Q and setting all other elements to cipher.

To discover the stationary probability distribution vector, we must next observe ${\displaystyle \varphi }$ such that

${\displaystyle \varphi S=\varphi ,}$

with ${\displaystyle \varphi }$ being a row vector, such that all elements in ${\displaystyle \varphi }$ are greater than 0 and ${\displaystyle \|\varphi \|_{1}}$ = 1. From this, π may be found as

${\displaystyle \pi ={-\varphi (\operatorname {diag} (Q))^{-1} \over \left\|\varphi (\operatorname {diag} (Q))^{-1}\correct\|_{1}}.}$

(S may exist periodic, even if Q is not. Once π is constitute, it must be normalized to a unit vector.)

Another discrete-time process that may exist derived from a continuous-time Markov chain is a δ-skeleton—the (detached-time) Markov chain formed past observing 10(t) at intervals of δ units of time. The random variables X(0),X(δ),X(2δ), ... give the sequence of states visited by the δ-skeleton.

See also [edit]

• Kolmogorov equations (Markov spring process)

Notes [edit]

1. ^ ^{a b} Ross, South.Yard. (2010). Introduction to Probability Models (ten ed.). Elsevier. ISBN978-0-12-375686-two.
2. ^ Norris, J. R. (1997). "Continuous-time Markov bondage I". Markov Chains. pp. 60–107. doi:10.1017/CBO9780511810633.004. ISBN9780511810633.
3. ^ Norris, J. R. (1997). "Continuous-time Markov chains II". Markov Chains. pp. 108–127. doi:10.1017/CBO9780511810633.005. ISBN9780511810633.

References [edit]

• A. A. Markov (1971). "Extension of the limit theorems of probability theory to a sum of variables connected in a chain". reprinted in Appendix B of: R. Howard. Dynamic Probabilistic Systems, book i: Markov Bondage. John Wiley and Sons.
• Markov, A. A. (2006). Translated by Link, David. "An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Bondage". Science in Context. xix (4): 591–600. doi:10.1017/s0269889706001074.
• Leo Breiman (1992) [1968] Probability. Original edition published past Addison-Wesley; reprinted by Society for Industrial and Applied Mathematics ISBN 0-89871-296-iii. (Encounter Chapter 7)
• J. L. Doob (1953) Stochastic Processes. New York: John Wiley and Sons ISBN 0-471-52369-0.
• S. P. Meyn and R. L. Tweedie (1993) Markov Chains and Stochastic Stability. London: Springer-Verlag ISBN 0-387-19832-vi. online: MCSS . Second edition to appear, Cambridge Academy Press, 2009.
• Kemeny, John G.; Hazleton Mirkil; J. Laurie Snell; Gerald Fifty. Thompson (1959). Finite Mathematical Structures (1st ed.). Englewood Cliffs, NJ: Prentice-Hall, Inc. Library of Congress Carte Itemize Number 59-12841. Classical text. cf Chapter vi Finite Markov Chains pp. 384ff.
• John Yard. Kemeny & J. Laurie Snell (1960) Finite Markov Chains, D. van Nostrand Company ISBN 0-442-04328-7
• E. Nummelin. "Full general irreducible Markov chains and non-negative operators". Cambridge University Press, 1984, 2004. ISBN 0-521-60494-10
• Seneta, E. Not-negative matrices and Markov bondage. second rev. ed., 1981, 16, 288 p., Softcover Springer Series in Statistics. (Originally published past Allen & Unwin Ltd., London, 1973) ISBN 978-0-387-29765-i

whiteleggehopearabits.blogspot.com

Source: https://en.wikipedia.org/wiki/Continuous-time_Markov_chain

Share this post